GAMES 101 课程笔记

这是正在学的 Games 101 图形学入门课程笔记，自己看的。在此留档，做测试和复习。

持续更新，欢迎评论！！！

GAMES中文官网链接

Lecture 01 Introduction

GAMES: Graphics And Mixed Environment Symposium
Rasterization 光栅化
online 实时渲染 30fps
offline 离线渲染
Curves and Meshes 曲线和曲面
Ray Tracing 光线追踪慢但是真实
- Trade of 取舍
- 可以实时光线追踪
Animation/Simulation 模拟动画仿真
Games 101 is not about
- using Opengl / DirectX / Vulkan 图形学 api
- the syntac of Shaders
- 学完自然会用
- 3D 建模和游戏开发 3D modeling using Maya / Blender or Unity / Unreal Engine or VR / game development
- Computer Vision / Deep Learning topics 计算机视觉，一切需要理解、猜测、翻译的东西
- Like Opencv
图形学：由模型到图像，或者对三维形体的理解和仿真
计算机视觉：从图像到模型，或者由图像分析之后生成图像（人脸 gan 生成人脸），三维重建
计算摄影学：拍照片的技术，类似计算机视觉

course logistics 课程具体细节

comprehensive but without hardware programming! without 3090!
References : Fundamentals of Computer Graphics
games-cn.org
Assignment: 有框架和明确描述，c++ 写哦
7 次小作业，每次不超过 20 行
用 eigen 库做矩阵向量运算
所有工业都有 c++ 编程图形学框架
提供一个虚拟机来跑，立刻着手开发
最后有一个大作业，融会贯通，自己做一个酷炫的东西，课程相关。
一定要使用 IDE 集成开发环境，方便
- Windows : Visual Studio, Visual Studio Code (cross platform) , Qt creator
- 不推荐: Clion, Eclipse
- 非常不推荐: Sublime Text, Vi / Vim, Emacs, Notepad++
geek = genius freak 天才和怪胎
学术诚信，代码框架不要给到 github 上，大作业可以发布
回答问题不要贴代码，回答问题本身。

Lecture 02 Review of Linear Algebra

向量 vector

向量基础知识
向量的加减法、点乘、叉乘
- 求两个向量的角度 -> 光栅化技术／光照模型
- 向量投影、向量分解 -> 金属光泽
- 向量叉乘 -> 三维空间的直角坐标系／右手坐标系
- 叉乘 -> 判定向量左右，判定点在三角形内外
- corner case 自己说了算
笛卡尔坐标系

矩阵 matrix

矩阵变换
矩阵一般没有交换律，有结合律，分配律
- y 轴对称矩阵
- 单位矩阵
- 转置矩阵 (AB)t=BtAt
- 矩阵的逆 -> 指挥相机的运动和旋转

Lecture 03 矩阵变换 Transformation

assignment 0

why study transformation

镜头移动
逆运动学
关节移动
3d to 2d projection 三维到二维投影

2D Transformations: rotation, scale, shear

均匀缩放矩阵：$\begin{pmatrix} s & 0 \\ 0 & s \end{pmatrix}$ 非均匀缩放矩阵：$\begin{pmatrix} s_x & 0 \\ 0 & s_y \end{pmatrix}$
对称矩阵：$\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}$
切变矩阵：$\begin{pmatrix} 1 & a \\ 0 & 1 \end{pmatrix}$
旋转矩阵（默认绕原点逆时针）$R_{\theta} = \begin{pmatrix}cos\theta&&-sin\theta\\ sin\theta&&cos\theta\end{pmatrix}$ 旋转矩阵的逆矩阵：$R_{\theta}^{-1} = \begin{pmatrix}cos\theta&&sin\theta\\ -sin\theta&&cos\theta\end{pmatrix} = R_{\theta}^{T}$ 因此旋转矩阵是正交的
变换的本质：$\begin{pmatrix}x’\\ y’\end{pmatrix} = \begin{pmatrix}a&b\\ c&d\end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}$ 既 $\boldsymbol{x’} = M\boldsymbol{x}$

homogeneous coordinate 齐次坐标

平移 $\begin{pmatrix}x’\\ y’ \end{pmatrix}= \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix}x \\ y \end{pmatrix} + \begin{pmatrix} t_x \\ t_y \end{pmatrix}$
alline map 仿射变换
有一个多余项，所以试图找到统一的解决方案，但是有代价（trade off / no free lunch theory） $$ \begin{pmatrix} x’ \\ y’ \\ 1 \\ \end{pmatrix} = \begin{pmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \\ \end{pmatrix} $$
先变换，后平移
2D point = $(x, y, 1)^t$
2D vector = $(x, y, 0)^t$
point diff with vector: vector the same, point diff
- vector + vector = vector
- point - point = vector
- point + vector = point
- point + point = midpoint
- in homogeneous coordinates: $$\begin{pmatrix}x \\ y \\ w \end{pmatrix} = \begin{pmatrix}x/w \\ y/w \\ 1 \end{pmatrix}$$
Inverse Transition
Composite Transform 矩阵乘法
sequence of affine transform 任意点旋转＝移到原点，旋转，移动回去

Lecture 04 3D transforms

3D transformations 3 维变换

3D points = $(x, y, z, 1)^T$ or $(x, y, z, w)^T(w \ne 0)$ 3D vector = $(x, y, z, 0)^T$
Scale 缩放

$$ \boldsymbol{S}(s_x, s_y, s_z) = \begin{pmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$

Translation 平移

$$ \boldsymbol{T}(t_x, t_y, t_z) = \begin{pmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$

Rotation 旋转（关于某个轴右手螺旋转 $\alpha$ 角）

$$ \boldsymbol{R}_x(\alpha) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & cos\alpha & -sin\alpha & 0 \\ 0 & sin\alpha & cos\alpha & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$

$$ \boldsymbol{R}_y(\alpha) = \begin{pmatrix} cos\alpha & 0 & sin\alpha & 0 \\ 0 & 1 & 0 & 0 \\ -sin\alpha & 0 & cos\alpha & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$

$$ \boldsymbol{R}_z(\alpha) = \begin{pmatrix} cos\alpha & -sin\alpha & 0 & 0 \\ sin\alpha & cos\alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$

$$ \boldsymbol{R}_{xyz}(\alpha, \beta, \gamma) = \boldsymbol{R}_x(\alpha) \boldsymbol{R}_y(\beta) \boldsymbol{R}_z(\gamma) $$

Rodrigues’ Rotation Formula
四元数（Quaternion）用作插值

Viewing transformation 观测变换

model / view / projection transformation (mvp transformation)

View / Camera transformation 视图变换

Define the camera
- Position $\vec{e}$
- Look-at / gaze direction $\hat{g}$
- Up direction (for rotation) $\hat{t}$
Default settings
- $\vec{e} \rightarrow (0, 0, 0)^T$
  ，相机位置移到原点
- $\hat{g} \rightarrow -Z = (0, 0, -1)^T$，相机看向 Z 轴负方向
- $\hat{t} \rightarrow Y = (0, 1, 0)^T$，相机的向上方向为 Y 轴正方向
- $\hat{g} \times \hat{t} \rightarrow X = (1, 0, 0)^T$
Transformation 变换方程：
$$ M_{view} = R_{view}T_{view} $$
$$ T_{view} = \begin{pmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$
$$ R_{view} = \begin{pmatrix} x_{\hat{g} \times \hat{t}} & x_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\ x_{\hat{t}} & y_{\hat{t}} & z_{\hat{t}} & 0 \\ x_{-\hat{g}} & y_{-\hat{g}} & z_{-\hat{g}} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$

Projection transformation 投影变换

3D to 2D

Orthographic projection 正交变换

特征

无近大远小关系，假设相机无限远，平行的投影到某平面内
多用于工程制图
逻辑上，丢掉 Z 轴方向，所有内容挤在 xy 平面上

步骤

目标：把一个大立方体 $[l,r]\times[b,t]\times[f,n]$ 平移并压缩到 canonical cube（正则、规范、标准立方体）$[-1, 1]^3$ 里面，由于我们看向 -Z 方向，所以坐标上 $Far < Near < 0$，也是为什么OpenGL等一些图形API用左手系。

先平移中心点到原点

$$ \begin{pmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$

再缩放到 $[-1, 1]^3$ ：

$$ \begin{pmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$

总变换矩阵：

$$ M_{ortho} = \begin{pmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} = \begin{pmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f} \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$

问题：

当被缩放到 $[-1, 1]^3$ 之后，原本物体被拉伸。之后会做一次视口变换，保证物体尺寸合适。
变换坐标系不好理解，不直观
输入给定
精度问题

Perspective projection 透视变换

特征

有近大远小关系，假设相机有限远，形成锥形投影到某平面内
视觉上平行线不再平行

步骤推导合理性，而非严格证明

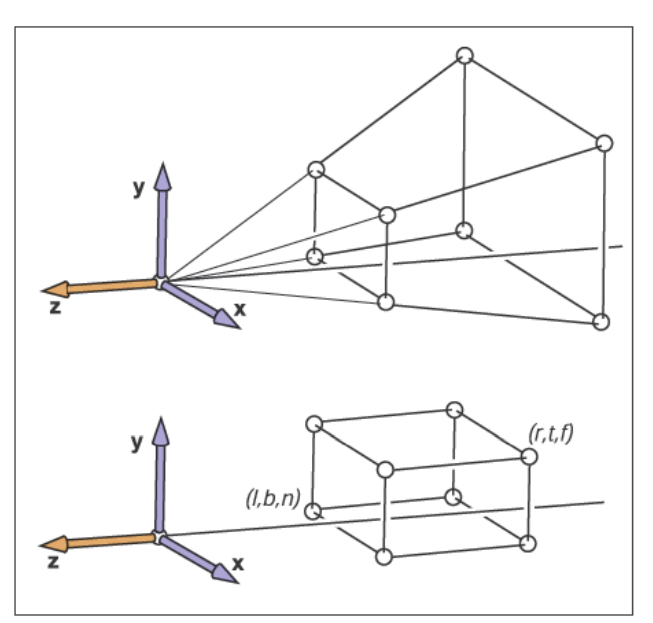
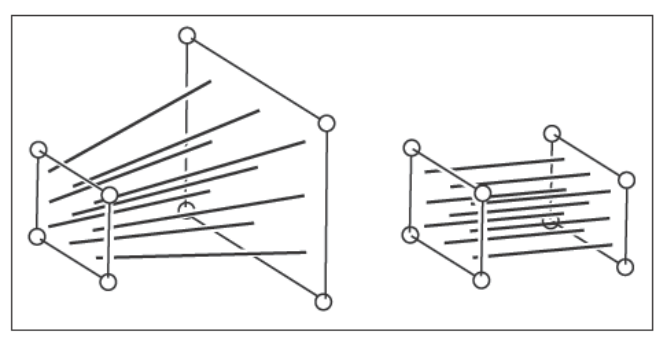
直观上，先把 $(n,f]$ 平面挤压：把锥体挤压成长方体，其中 $n \rightarrow n, f \rightarrow f, M_{persp \rightarrow ortho}$ 透视投影1 透视投影2

规定：

近平面里任何个点不变
远平面位置不变，但是向中心收缩，且中心点不变

设近平面上一点 $(x’, y’, z’)$ 和远平面（或者内部某个平面）上一点 $(x, y, z)$ 在一条直线上，由相似三角形关系有 $y’=\frac{n}{z}y$，且 $x’=\frac{n}{z}x$，则由其次坐标表示之后

$$ \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} \frac{nx}{z} \\ \frac{ny}{z} \\ unknown \\ 1 \end{pmatrix} == \begin{pmatrix} nx \\ ny \\ unknown \\ z \end{pmatrix} $$

可以得到： $$ M_{persp \rightarrow ortho} = \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} $$

近平面上的点不会变，即

$$ \begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} == \begin{pmatrix} nx \\ ny \\ n^2 \\ n \end{pmatrix} $$

因为第三行乘积得到 $n^2$，所以 $M_{persp \rightarrow ortho}$ 第三行只能是 $\begin{pmatrix} 0 & 0 & A & B \end{pmatrix}$，其中 A 和 B 未知。

$$ \begin{pmatrix} 0 & 0 & A & B \end{pmatrix} \begin{pmatrix} x \\ y \\ n \\ 1 \\ \end{pmatrix} = n^2 \Rightarrow An + B = n^2 $$

此时弹幕提出问题，说如果是形如 $\begin{pmatrix} \frac{pn^2}{x} & \frac{qn^2}{y} & A & B \end{pmatrix}$ 的形式（其中 $p, q$ 为常数），也可以得到右边只有 $n^2$ 的形式。实际上不可能，因为左式是变换矩阵，一定是一个常量矩阵，不能含有 $x, y$ 等变量。

同理，远平面上的 z 参数不发生变化，考虑中间的 $(0, 0)$ 点不变，即

$$ \begin{pmatrix} 0 \\ 0 \\ f \\ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} 0 \\ 0 \\ f \\ 1 \end{pmatrix} == \begin{pmatrix} 0 \\ 0 \\ f^2 \\ f \end{pmatrix} \Rightarrow Af+B=f^2 $$

解方程可得

$$ \begin{cases} A = n + f \\ B = -nf \\ \end{cases} $$

则

$$ M_{persp \rightarrow ortho} = \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n + f & -nf \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} $$

再正交变换到 $[-1, 1]^3$

$$ M_{persp} = M_{ortho}M_{persp \rightarrow ortho} \\ = \begin{pmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f} \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n + f & -nf \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} \\ = \begin{pmatrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0 \\ 0 & 0 & \frac{n+f}{n-f} & -\frac{2nf}{n-f} \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} $$

问题：对于中间的任何一个点 $(x, y, z)$， $z$ 会靠近近平面还是靠近远平面？值变大还是变小？

$$ z’=\frac{n+f}{n-f}z-\frac{2nf}{n-f} \\ z’-z=\frac{2f(z-n)}{n-f}>0 \\ 0 > n > z’ > z > f $$

答：靠近，变大

特殊的，当 $l=-r,b=-t$ 时：

$$ M_{persp} = \begin{pmatrix} \frac{n}{r} & 0 & 0 & 0 \\ 0 & \frac{n}{t} & 0 & 0 \\ 0 & 0 & \frac{n+f}{n-f} & -\frac{2nf}{n-f} \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} $$

Lecture 05 Rasterization 1 (Triangle)

BBS上讨论很踊跃，提问的艺术

透视投影之后，就是把物体画到屏幕上，这时就是光栅化技术

定义两个概念：

长宽比 aspect ratio = width / height
（垂直的）可视角度 vertical field-of-view fovY，和水平的可视角度可以相互转化

和变换一样，已知 $(r, l),(t, b),(n,f)$ 六个参数，要把长宽比和可视角度用这六个参数表示（假设屏幕中心对称，即 $l=-r,b=-t$ ） $$ \tan{\frac{fovY}{2}}=\frac{t}{\lvert n \rvert} \\ aspect=\frac{r}{t} $$

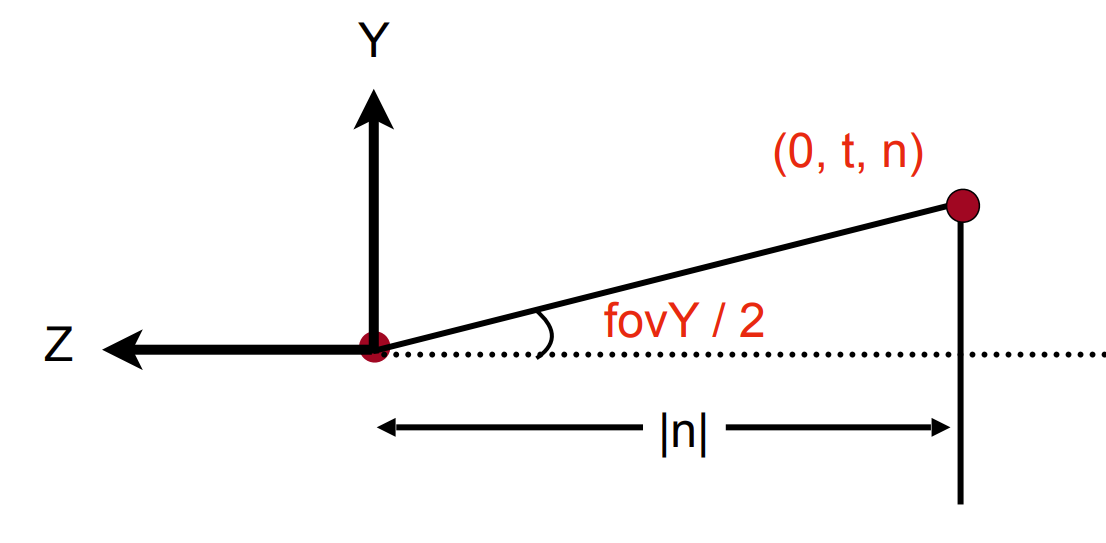
screen 屏幕

定义：

一个像素形成的数组
数组的大小取决于分辨率（如 1920 × 1080 ）
一种光栅成像设备（raster display，raster 是德语中 screen 的意思）

像素：

同一色彩的最小单位
一个像素可以用 $(R, G, B)$ 表示
像素的坐标用 $(x, y)$ 整数表示，下表范围是 $[(0,0),(width-1,height-1)]$ ，中心点在 $(x+0.5,y+0.5)$ ，覆盖了 $(0,0)-(width,height)$

保持 $z$ 不变，把 $[-1,1]^2$ 拉伸到 $[0,width] \times [0,height]$ ，称之为视口变换： $$ \begin{pmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2} \\ 0 & \frac{height}{2} & 0 & \frac{height}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$ 仍然是空间中三角形、多边形等信息，接下来就要离散化成为像素。

绘图机器 Drawing Machine

比如打印机、绘图机机器人、激光切割等

不同的光栅化显示设备

示波器 Oscilioscope
阴极射线管显示器 Cathode Ray Tube CRT ，比较伤眼睛
- 为了画的块，可以隔行扫描，利用人眼视觉暂留
- 但是隔行扫描可能会造成严重的画面撕裂，尤其对于高速运动的视频
显示器，通过内存或显存中的一块区域映射到屏幕上，叫做 Frame Buffer
平板显示设备
- 低分辨率 LCD 显示器
- 手机：高分辨率 LCD 显示器，视网膜屏幕
- OLED 显示器等等
LCD （Liquid Crystal Display）液晶显示设备
- 液晶的排布影响光的偏振方向，本质上是圆偏振光，来控制出光亮
LED （Light emitting diode）Array Display 发光二极管
电子墨水屏，控制黑墨水和白墨水的朝向，刷新率很低

用三角形作为模型的基础单元

为什么用三角形：

多边形都可以又三角形组成
三角形内部一定是平面，不会有凹凸
三角形内外定义明确，容易（用叉积）判断点是否在三角形内部
三角形内部插值

采样 Sampling

采样：函数离散化的方法

采样是图形学里很重要的概念，时间、区域、位置、物体表面反射等性质都需要采样

取一个平面内三角形，定义一个函数来判断一个像素中心点是否在三角形内，这是一种采样

1
2
3
4
5
bool inside(tri, x, y); // definition

for (int x = 0; x < xmax; ++x)
    for (int y = 0; y < ymax; ++y)
        image[x][y] = inside(tri, x + 0.5, y + 0.5); // central points

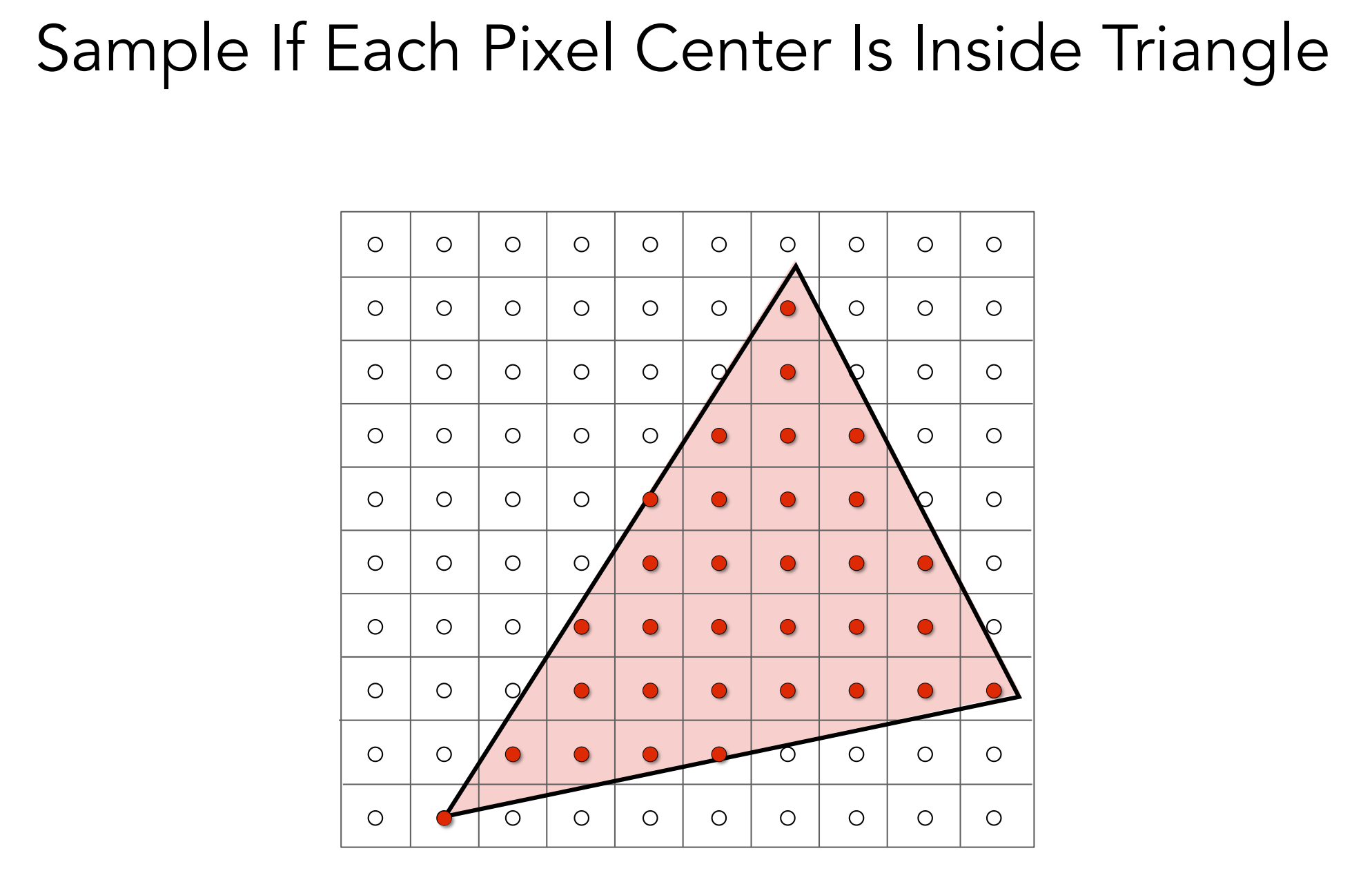
inside函数的实现：应用叉乘的性质。定义三角形 $\triangle P_0P_1P_2$ ，顶点逆时针方向排布；定义一个判断的点 $Q$。如果下列条件都满足： $$ z(\vec{P_0P_1} \times \vec{P_0Q}) > 0 \\ z(\vec{P_1P_2} \times \vec{P_1Q}) > 0 \\ z(\vec{P_2P_0} \times \vec{P_2Q}) > 0 \\ $$ 则点 $Q$ 在三角形 $\triangle P_0P_1P_2$ 内，否则在三角形外。或者三角形顺时针定义，若以上全部小于零，则在三角形内。

如果一个点在三角形边界上，在这门课上不做处理，在其他的地方可能会特殊处理，比如在OpenGL等图形学API上有严格的定义（规范）。

优化：可以用三角形的轴向包围盒（axis-aligned Bounding Box，缩写AABB）来优化循环。

更优化：取每一行的轴向包围和，适用于旋转45度而且窄长的三角形

实际上的像素排列

三星 OLED 钻石排列中，红色：蓝色：绿色=1:1:2，因为人对于绿色最敏感

问题

如果仅仅会出现走样或锯齿（Aliasing or Jaggies），所以图形学的一大重点就在于抗锯齿或者反走样，这是下节课的内容

Lecture 06 Rasterization 2 (Antialiasing and Z-Buffering)

上节课使用采样技术，会出现明显的锯齿（jaggies）

采样理论 Sampling

照片：对于到达传感器的光照信息采样

视频：在时间中采样（动画定义在帧上）

采样瑕疵 Sampling Artifacts

锯齿 Jaggies
摩尔纹 Moire Pattern：删除奇数行和奇数列并且缩放到原来大小
人眼在时间中的采样，跟不上旋转的速度（顺时针变逆时针、原力直升机等）

本质上就是信号的变化太快，采样跟不上

反走样思路

滤波

在采样之前，做一个模糊（滤波）操作，用来抗锯齿（反走样）

先采样再模糊（Blutted Aliasing），不行！

原理

频域 Frequency Domain

定义频率 $f$，有 $\cos{2\pi fx}$，$f=\frac{1}{T}$。

傅里叶展开：$f(x)=\frac{a_0}{2}+\sum_{n=1}^{+\infty}[{a_n \cos{n\omega t}}+ {b_n \sin{n\omega t}}]$，任何一个函数都能分解成不同的频率（频率从低到高的形式）

傅里叶展开和傅里叶变换紧密相连，对于固定的采样频率，低频信号采样能恢复，高频信号采样可能不能恢复，而是变成低频信号。采样频率和信号频率紧密相关。

走样：两种频率的信号采样得到完全一样的结果，叫做走样。（Alisaing 相似）

滤波 filter

定义：删除特定频率的信号。傅里叶变换可以把时域变到频域。傅里叶变换一张图会发现，低频信息非常多，集中在中间，高频信息非常少，分散在四周。频谱。

高通滤波器：删除低频信号，得到高频信号。用于提取人物边界（人物与背景的边缘信息）。

低通滤波器（blur）：删除高频信号，得到低频信号。用于模糊信息（马赛克，磨皮等等）。

高通低通滤波器：删除高低频信息，得到中频信息。

《数字图像处理》

目前多数的图像操作是机器学习。

滤波 Filtering = 平均 Averaging = 卷积 Convolution

卷积

定义一个一位数组，有一个窗口在数组上滑动。窗口的定义为：

1
b[i] = 0.25 * a[i-1] + 0.5 * a[i] + 0.25 * a[i+1];

类似于做一个平均，这个窗口叫卷积核。卷积滤波 = 均值滤波

卷积定理：时域的卷积等于频域的乘积

Box Filter 盒子滤波器 = 低通滤波器

盒子时域变大了，盒子的频域变小了。用越大的卷积核去做卷积操作，基本上都一样了，说明低频信号多，高频信号少。

采样

采样就是重复原始信号频域上的内容。

对于任意一个函数，乘以冲击函数 $P_{\theta}(t)$

为什么会产生走样现象（奈奎斯特采样定律）：时域上采样的间隔变大（变慢），频域上复制的间隔变小，会有频率重叠（混叠）在一起，导致走样。

反走样

增加采样率

增加分辨率，1080P -> 4k。

低通滤波器

先把一个信号高频信息拿掉，再采样。

实际上对边缘做卷积。比如取个 3*3 的方格作为低通滤波器，对采样函数 f(x, y) 做卷积操作，

实际上

MSAA

Multisample Antialiasing 多重采样反走样（超采样），解决信号模糊操作，隐含的最后的采样操作。

原理：在一个像素中间多加几个采样点，应用采样函数，然后去平均。例如。如果一个像素覆盖0, 1, 2, 3, 4个采样点，就用对应的灰度值来填充像素。本质上是软件上的增加分辨率。

代价：超采 $n$ 倍，增大到 $n^2$ 倍的计算量。

工业界

用不同的样本分布，多个采样点可以复用。

FXAA

Fast Approximate AA 快速近似反走样。（先采样，找到边界，换成没有锯齿的边界）

TAA

Temporal AA 时间反走样。（复用上一帧的的边界，适用于静态变化的图像）

超分辨率

从低分辨率到高分辨率，要解决低分辨率下采样不够的问题。

DLSS

Deep Learning Super Sampling 深度学习超分辨率。

深度学习 = 猜。